SMT and Model Checkers

The next steps up for tree searchers and SAT solvers:

• State more complex than just truth tables
• Searching a graph instead of a tree
• Temporal logic

Technical Lingo

Satisfiability Modulo Theories (SMT) Problem

Decision problem for logical first order formulas with respect to combinations of background theories such as: arithmetic, bit-vectors, arrays, and uninterpreted functions.

Dining Philosophers

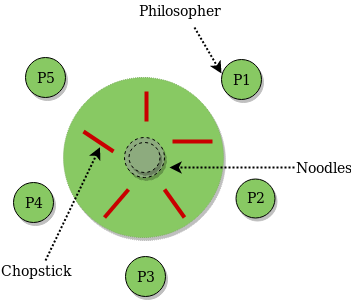
Core model:

State of one chopstick ∈ { Unused, LeftPhilosopher, RightPhilsopher }

State of all chopsticks ∈ {'UUUUU', 'UUUUL', 'UUURL', 'RUURL', ... }

Number of possible states:  3⁵ = 243

Implied states for a philosopher:
    0 chopsticks held ⟶  Thinking
    1 chopsticks held ⟶  Trying to eat
    2 chopsticks held ⟶  Eating

Unconstrained chopstick state transitions:
    Unused ⟶  LeftPhilosopher
    Unused ⟶  RightPhilsopher
    LeftPhilosopher ⟶  Unused
    RightPhilsopher ⟶  Unused

Constrain the model with philosopher strategies:

Strategy D:
    0 chopsticks held ⟶  AcquireLeft
    1 chopsticks held ⟶  AcquireRight
    2 chopsticks held ⟶  ReleaseBoth

Strategy S:
   Philosopher zero always holds left chopstick

Strategy H:
    0 chopsticks held ∧ no request  ⟶  Enqueue an eat request
    0 chopsticks held ∧ requested but not available ⟶  Wait
    0 chopsticks held ∧ requested available ⟶  AcquireLeft
    1 chopsticks held ⟶  AcquireRight
    2 chopsticks held ⟶  ReleaseBoth

What the Solver Does

The transitions generate a graph.

The solver traverses the graph to see if: 1) every state has an exit state – deadlocks 2) every path loop has every philosopher eating – no one starves

Unlike the puzzle solvers, we need “temporal operators” that check the relationship between a succession of states:

Predicate P is always true.

A chopstick is held by 0 or 1 philosophers

Predicate P is eventually true

A philosopher with a left chopstick eventually gets a right one

Predicate P is always eventually true

After eating, a philosopher is always able to eat again

For example:

UUUUU -> ... -> UURLU ->  ULUUU -> ... -> UURLU -> ...
                   ^                         ^
                   |                         |
                P₃ eats   P₃ thinks       P₃ eats

TLA⁺ model checker

The TLA⁺ model checker generate the contrained graph, follows all paths, and checks all of the temporal invariants.

Here’s PlusCal model for the dining philosophers problem.

For a nice write-up on using TLA⁺ for the dining philosophers problem see the blog post by Murat Demirbas at http://muratbuffalo.blogspot.com/2016/10/modeling-dining-philosophers-algorithm.html

Other Tools

The Z3Py package lets you drive Microsoft’s Z3 solver, a production ready powerful SMT solver.

To get started, see this tutorial: https://ericpony.github.io/z3py-tutorial/guide-examples.htm